Trong phần mềm SPSS (và trong thống kê nói chung), hai khái niệm hệ số Sig. và hệ số p-value thực ra là một — chỉ khác về cách ghi.
Trong quá trình xử lý dữ liệu bằng phần mềm SPSS, đặc biệt khi thực hiện các phép kiểm định thống kê như Independent Sample T-test, ANOVA, Regression, hay Correlation, bạn sẽ thường thấy xuất hiện một cột hoặc một giá trị mang tên Sig. hoặc Sig. (2-tailed). Đây chính là giá trị p-value, hay còn gọi là mức ý nghĩa thống kê – yếu tố quyết định xem kết quả kiểm định của bạn có “ý nghĩa” hay không.
1. Khái niệm cơ bản về hệ số Sig. (p-value)
P-value (viết tắt của Probability Value, còn được gọi là Hệ số Sig. - viết tắt của Significance) là một đại lượng thống kê dùng trong kiểm định giả thuyết. Nó cho biết xác suất để xảy ra sai lầm khi bác bỏ giả thuyết gốc H₀ trong khi H₀ là đúng (giả thuyết đối là H₁).
Nói đơn giản hơn, hệ số Sig. cho biết mức độ tin cậy của kết quả kiểm định, giá trị sig. dao động trong khoảng từ 0 đến 1.
- Nếu Sig. nhỏ, nghĩa là xác suất sai lầm khi bác bỏ giả thuyết gốc là rất thấp → kết quả có ý nghĩa thống kê.
- Nếu Sig. lớn, nghĩa là chưa đủ bằng chứng để bác bỏ giả thuyết gốc → kết quả không có ý nghĩa thống kê.
Ta thường so sánh Sig. với mức ý nghĩa α (thường là 0.05) để quyết định:
Nếu Sig. ≤ 0.05 → bác bỏ H₀ → có ý nghĩa thống kê.
Nếu Sig. > 0.05 → chấp nhận H₀ → không có ý nghĩa thống kê.
Các phần mềm như AMOS, SmartPLS, Stata... hay sử dụng ký hiệu p-value, còn SPSS sử dụng ký hiệu là Sig.. Một số bảng kết quả trong SPSS hiển thị Sig. (2-tailed) hoặc Sig. (1-tailed). Nếu chỉ hiển thị Sig mà không phân ra 2-tailed hay 1-tailed nghĩa thì Sig. đó là Sig. (2-tailed).
2. Khác biệt Sig. (2-tailed) và Sig. (1-tailed)
Một số bảng kết quả trong SPSS thay vì dùng Sig. mà có các ký hiệu Sig. (2-tailed) hoặc Sig. (1-tailed).
a. Sig. (2-tailed) — Kiểm định hai phía
Dùng khi giả thuyết thay thế H₁ không xác định hướng (chỉ biết có khác biệt hoặc có tương quan, nhưng không biết lớn hơn hay nhỏ hơn).
Ví dụ về kiểm định trung bình bằng nhau giữa 2 nhóm dữ liệu:
H₀: μ₁ = μ₂
H₁: μ₁ ≠ μ₂
Khi đó ta dùng Sig. (2-tailed) vì kết quả có thể lệch theo hai hướng (lớn hơn hoặc nhỏ hơn).
Đây là loại kiểm định phổ biến nhất trong SPSS vì nó khách quan, ít sai sót hơn.
b. Sig. (1-tailed) — Kiểm định một phía
Dùng khi giả thuyết thay thế H₁ có hướng rõ ràng (kỳ vọng một nhóm lớn hơn nhóm kia, hoặc tương quan dương/âm).
Ví dụ về kiểm định trung bình khác nhau giữa 2 nhóm dữ liệu:
H₀: μ₁ ≤ μ₂
H₁: μ₁ > μ₂
Khi đó chỉ xét một phía của phân phối, nên xác suất Sig. (1-tailed) sẽ bằng một nửa Sig. (2-tailed).
Dạng kiểm định này mạnh hơn nếu hướng giả thuyết đúng, nhưng rủi ro sai lệch cao hơn nếu hướng giả định sai.
| Đặc điểm | Sig. (1-tailed) | Sig. (2-tailed) |
|---|---|---|
| Hướng giả thuyết | Có hướng (>, <) | Không có hướng (≠) |
| Vùng kiểm định | Một phía | Hai phía |
| Giá trị p | Bằng ½ của 2-tailed | Lớn gấp đôi 1-tailed |
| Mức độ chặt chẽ | Ít chặt hơn | Chặt chẽ hơn |
| Dùng trong SPSS | Khi giả thuyết có hướng | Mặc định, thông dụng |
3. Hệ số Sig. trong các phân tích cụ thể của SPSS
a. Kiểm định T-Test
Lấy ví dụ với kiểm định Paired-Sample T Test, đây là phép kiểm định thống kê dùng để so sánh giá trị trung bình của cùng một nhóm đối tượng ở hai thời điểm khác nhau hoặc hai điều kiện đo khác nhau.
Ví dụ trong ảnh bên dưới:
Giả thuyết H₀: Không có sự khác biệt trung bình giữa hai khảo sát.
Giả thuyết H₁: Có sự khác biệt trung bình giữa hai khảo sát.
Giá trị sig trong bảng Paired Samples Test bằng 0.000 < 0.05, bác bỏ giả thuyết H₀, nghĩa là có khác biệt một cách có ý nghĩa thống kê trung bình giữa hai biến KhaoSat1 và KhaoSat2.
b. Phân tích tương quan Pearson Correlation
Kết quả tương quan Pearson thể hiện một cặp biến có mối tương quan tuyến tính với nhau hay không.
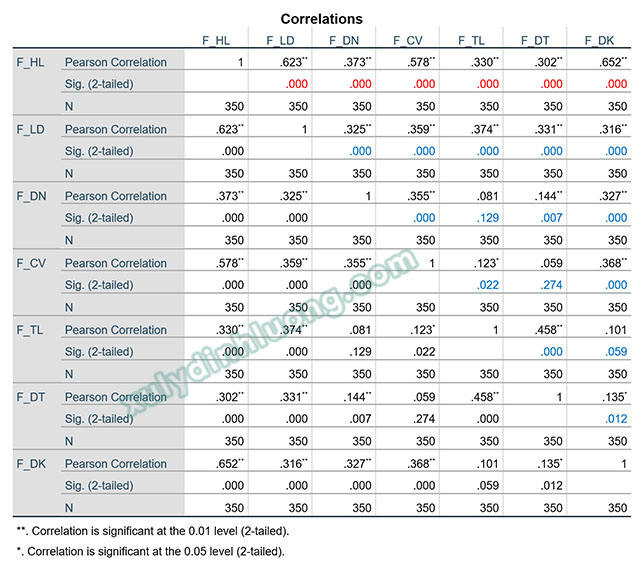
Ví dụ trong ảnh bên dưới xét cặp tương quan giữa F_LD với F_HL:
Giả thuyết H₀: Không có sự tương quan giữa F_LD và F_HL.
Giả thuyết H₁: Có sự tương quan giữa F_LD và F_HL.
Giá trị sig trong bảng Correlation của cặp biến F_LD và F_HL bằng 0.000 < 0.05, bác bỏ giả thuyết H₀, nghĩa là có mối tương quan giữa F_LD và F_HL.
c. Phân tích hồi quy Regression
Một trong các kết quả mà hồi quy trong sẽ đánh giá là các biến độc lập có sự ảnh hưởng lên biến phụ thuộc hay không.
Ví dụ trong ảnh bên dưới xét sự tác động từ biến độc lập F_DN lên biến phụ thuộc F_HL:
Giả thuyết H₀: Không có sự tác động từ F_DN lên F_HL.
Giả thuyết H₁: Có sự tác động từ F_DN lên F_HL.
Giá trị sig trong bảng Coefficients của F_DN bằng 0.777 > 0.05, chấp nhận giả thuyết H₀, nghĩa là không có sự tác động từ F_DN lên F_HL.
4. Các mức diễn giải phổ biến của p-value (Sig.) trong SPSS
| Giá trị p-value | Mức ý nghĩa | Diễn giải |
|---|---|---|
| Sig. < 0.001 | *** | Rất có ý nghĩa thống kê (99.9%) |
| Sig. < 0.01 | ** | Có ý nghĩa ở mức 99% |
| Sig. < 0.05 | * | Có ý nghĩa ở mức 95% |
| Sig. ≥ 0.05 | Không có ý nghĩa thống kê |
Trong kiểm định thống kê, ta luôn bắt đầu bằng hai giả thuyết:
- H₀ (Giả thuyết gốc): Không có sự khác biệt / Không có mối quan hệ
- H₁ (Giả thuyết thay thế): Có sự khác biệt / Có mối quan hệ
SPSS tính p-value để giúp ta quyết định giữa hai giả thuyết này.
Sig. < 0.05: Bác bỏ H₀ → chấp nhận H₁ → Kết quả có ý nghĩa.
Sig. ≥ 0.05: Không bác bỏ H₀ → Kết quả không có ý nghĩa.
Nhớ rằng: p-value không đo mức độ mạnh của tác động, mà chỉ cho biết sự tồn tại của tác động.