Kiểm định Bootstrap trên AMOS là một kỹ thuật mạnh để hỗ trợ xử lý mô hình SEM khi dữ liệu vi phạm phân phối chuẩn đa biến, cũng như hỗ trợ phân tích tác động gián tiếp trong mô hình. Bài viết này tác giả sẽ đi sâu vào phân biệt SEM thông thường và SEM bằng Bootstrap trên AMOS để các bạn hiểu rõ hơn khi nào sẽ sử dụng Bootstrap.
1. Công thức C.R = Bias/SE-Bias < 1.96 không có nguồn trích dẫn
Một số bài viết, video hướng dẫn, một số luận thạc sĩ tại Việt Nam đang đưa ra một chỉ số gọi là C.R = Bias/SE-Bias từ kết quả Bootstrap Standard errors của AMOS rồi so sánh nó với 1.96 (hoặc 2) như một tiêu chí chấp nhận hay bác bỏ ý nghĩa quan hệ trong mô hình. Đây là một cách đánh giá SAI HOÀN TOÀN của ứng dụng Bootstrap trong AMOS.
Những bài viết, các luận văn thạc sĩ này đưa ra các nguồn như Anderson & Gerbing (1998), Schumacker & Lomax (1996), Byrne (2016)... Tuy nhiên, toàn bộ các tác giả này hoàn toàn không hề đưa ra công thức này. Các bạn có thể tìm kiếm trên internet các ấn phẩm dạng PDF của những công trình trên để tự kiểm chứng lại.
Công thức C.R = Bias/SE-Bias so với 1.96 này duy nhất chỉ có ở luận văn tại Việt Nam, các bạn tìm kiếm các bài giảng trên Youtube các giáo sư nước ngoài, hay các sách về AMOS trên Thế giới có lượt trích dẫn nhiều, các tạp chí lớn có sử dụng AMOS trong phân tích mô hình SEM đều không sử dụng công thức này. Nếu đây là một công thức đúng dùng để đánh giá ý nghĩa quan hệ trong mô hình SEM, tại sao các bài giảng của giáo sư nước ngoài không đề cập đến? Tại sao các sách uy tín về AMOS trên Thế giới không nêu ra? Tại sao các tạp chí uy tín có ứng dụng AMOS không sử dụng?
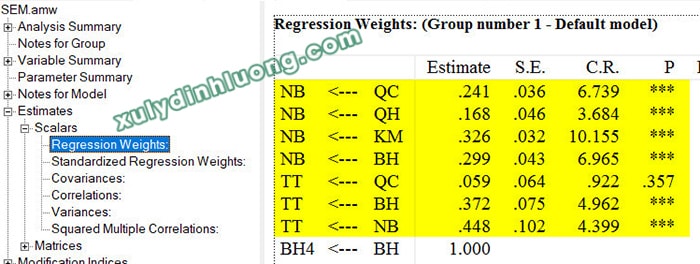
C.R là viết tắt của Critical Ratio = Chỉ số đánh giá/Sai số chuẩn của chỉ số chính là công thức tính t-value để kiểm định xem Chỉ số đánh giá có khác 0 hay không. Ví dụ, trong bảng bên dưới là kết quả bảng hệ số tác động chưa chuẩn hóa trong phân tích SEM. Tác động NB ← QC có hệ số tác động (Estimate) là 0.241 và sai số chuẩn (S.E) là 0.036, thực hiện phép tính C.R = Chỉ số/Sai số chuẩn của chỉ số tương đương C.R = Estimate/S.E = 0.241/0.036 = 0.694 ~ 0.67 chính là giá trị C.R trong bảng bên dưới. Có sự sai lệch một chút ở đây bởi vì các giá trị Estimate và S.E trong bảng hiển thị là giá trị làm tròn 3 số thập phân, còn C.R ở phần mềm tính toán thì tính luôn một dãy các con số thập phân phía sau. Sau khi tính ra C.R, chúng ta mang đi tra bảng phân phối student để dò ý nghĩa kiểm định, thì giá trị C.R hay t-value = 1.96 chính là ngưỡng p-value = 0.05 (cột P cuối cùng ở bảng bên dưới). Nếu C.R lớn hơn 1.96 (p-value < 0.05) thì giá trị ở Estimate khác 0 một cách có ý nghĩa. Nếu C.R nhỏ hơn 1.96 (p-value > 0.05) thì giá trị ở Estimate bằng 0 một cách có ý nghĩa.
Áp dụng vào công thức C.R = Bias/SE-Bias nghĩa là chúng ta đang đi kiểm định xem độ chệch Bias trong công thức này có bằng 0 hay không.
- Bias: chênh lệch giá trị hệ số tác động từ trung bình cộng các mẫu Bootstrap so với hệ số tác động từ SEM mẫu gốc.
- SE-Bias: sai số chuẩn của Bias
Độ chệch Bias của một kết quả Bootstrap nhỏ luôn là một điều tốt, Bias tiến về 0 là một điều tốt cho thấy phần lấy mẫu của Bootstrap khá đồng đều. Nhưng nó chỉ dừng ở việc đánh giá sự lấy mẫu lặp lại của Bootstrap có ổn định hay không như vậy thôi, chứ nó không phải là một tiêu chí để chấp nhận hay bác bỏ ý nghĩa một quan hệ tác động trong mô hình. Kết quả tính toán C.R = Bias/SE-Bias của quan hệ tác động đó nhỏ hay lớn hơn 1.96 cũng không liên quan gì việc kết luận quan hệ đó có ý nghĩa hay không có ý nghĩa. Kết quả từ phân tích SEM là bạn đã kết luận xong mô hình rồi, không cần triển khai thêm Bootstrap nếu bạn không phân tích quan hệ trung gian. Còn vì sao chạy SEM rồi kết luận mô hình mà không triển khai Bootstrap nữa có 2 lý do:
1. Công thức C.R = Bias/SE-Bias là một công thức đúng nhưng không phải ứng dụng làm một tiêu chí kết luận quan hệ trong mô hình có ý nghĩa hay không có ý nghĩa. Nên không cần phải chạy Bootstrap để tính toán chỉ số này.
2. Bootstrap là một kỹ thuật đánh giá quan hệ trực tiếp thay thế kiểu đánh giá của SEM mặc định trên AMOS. Hai loại kỹ thuật này thay thế cho nhau chứ không xuất hiện cùng lúc với nhau khi đánh giá tác động trực tiếp trên mô hình. Việc bạn đưa cả 2 vào trong một phần trình bày định lượng đã là không phù hợp rồi. Chi tiết bạn xem tiếp các mục phía sau.
2. Giả định phân phối chuẩn đa biến trong phân tích AMOS
Kiểm định SEM thông thường trong AMOS là một kỹ thuật thống kê mạnh mẽ dùng để kiểm tra mối quan hệ giữa các biến tiềm ẩn (latent variables) và các biến quan sát (observed variables) trong mô hình sử dụng phương pháp ước lượng Maximum Likelihood làm mặc định. Phương pháp ước lượng này yêu cầu dữ liệu phải có phân phối chuẩn đa biến - multivariate normality (Barbara M. Byrne, 2016; Joel Collier, 2020).
Tuy nhiên trên thực tế, hầu hết dữ liệu không thể đáp ứng được giả định phân phối chuẩn đa biến này (West và cộng sự, 1995). Việc đánh giá các quan hệ trong mô hình bằng phương pháp Maximum Likelihood sẽ dẫn đến các sai lệch ước lượng. Và sự xuất hiện của Bootstrap (Hancock & Liu, 2012; West và cộng sự, 1995; Yung & Bentler, 1996; Zhu, 1997) chính là một hướng tiếp cận tối ưu nhất cho tới hiện tại để xử lý vấn đề dữ liệu vi phạm phân phối chuẩn đa biến.
Kiểm định Bootstrap trong AMOS là một phương pháp thống kê không tham số (non-parametric) được sử dụng rộng rãi để ước lượng độ tin cậy của các tham số trong mô hình thống kê. Thay vì dựa vào các giả định về phân phối của dữ liệu, Bootstrap tiến hành lấy mẫu lại (resampling) từ dữ liệu ban đầu để tạo ra nhiều mẫu dữ liệu mới. Từ đó, ta có thể tính toán lại các tham số trên mỗi mẫu mới và sử dụng phân phối của các ước lượng này để đánh giá độ tin cậy của ước lượng ban đầu. Bootstrap không cần giả định phân phối chuẩn dữ liệu đầu vào.
Để tránh nhầm lẫn về thuật ngữ, tác giả đặt 2 tên gọi sau:
- SEM-Maximum Likelihood (SEM thông thường) phương pháp ước lượng mô hình SEM mặc định của AMOS mà chúng ta thường sử dụng.
- SEM-Bootstrap: phương pháp ước lượng mô hình SEM bằng kỹ thuật Bootstrapping.
3. Sử dụng SEM-Maximum Likelihood hay SEM-Bootstrap?
2.1 Sự khác biệt giữa SEM-Maximum Likelihood và SEM-Bootstrap
Cả SEM-Maximum Likelihood và SEM-Bootstrap đều có cùng chức năng là đánh giá ý nghĩa thống kê của những quan hệ tác động trong mô hình. Tuy nhiên, giả định dữ liệu đầu vào cũng như cơ chế đánh giá của hai kỹ thuật này khác nhau, cùng xem qua bảng so sánh bên dưới:
| Yếu tố | SEM-Maximum Likelihood | SEM-Bootstrap |
|---|---|---|
| Phương pháp ước lượng | Maximum Likelihood (ML) | Bootstrap |
| Yêu cầu về phân phối dữ liệu | Phân phối chuẩn đa biến | Không yêu cầu phân phối chuẩn |
| Ước lượng tham số | Trực tiếp từ dữ liệu gốc | Từ các mẫu Bootstrap |
| Sai số chuẩn | Ước lượng từ dữ liệu gốc | Sai số chuẩn Bootstrap (SE-Bias) |
| Khoảng tin cậy | Dựa trên phân phối chuẩn | Khoảng tin cậy Bootstrap |
| Kiểm định ý nghĩa thống kê | Dựa trên phân phối chuẩn | Dựa trên phân phối của các mẫu Bootstrap |
| Khi nào sử dụng | Dữ liệu có phân phối chuẩn | Dữ liệu không có phân phối chuẩn, kích thước mẫu nhỏ |
2.2 Nếu dữ liệu không có phân phối chuẩn đa biến thì thực hiện SEM-Maximum Likelihood được không?
Như đã đề cập ở mục đầu, nghiên cứu của West và cộng sự (1995) nêu rằng hầu hết dữ liệu trên thực tế đều vi phạm giả định phân phối chuẩn đa biến, trong khi đó SEM thông thường cần dữ liệu đảm bảo điều kiện này, vậy thì SEM thông thường không thể sử dụng được?
Có rất nhiều nghiên cứu đăng tải trên các tạp chí lớn, luận văn thạc sĩ, luận án tiến sĩ thực hiện SEM thông thường trên AMOS để đánh giá quan hệ tác động trong mô hình mà không kiểm tra xem dữ liệu có đảm bảo giả định phân phối chuẩn đa biến hay không. Đây là cách làm không đúng nhưng vẫn được sử dụng rộng rãi bởi vì:
(1) Sự tiếp nối cái sai từ người đi trước.
Giai đoạn từ sau năm 2000, các công trình nghiên cứu về giả định phân phối chuẩn đa biến trong SEM thông thường mới được đề cập nhiều, còn ở giai đoạn trước đó, giả định này ít được quan tâm. Do đó, một số nhà nghiên cứu không biết được rằng phải đảm bảo giả định này thì SEM thông thường mới nên được thực hiện.
Về sau, các nghiên cứu mới thừa kế lại các công trình nghiên cứu này và không đi sâu vào các giả định của SEM-Maximum Likelihood, dẫn đến sai nối tiếp sai.
(2) Rất khó khăn để có được một bộ dữ liệu có phân phối chuẩn đa biến.
Như West và cộng sự (1995), Barbara M. Byrne (2016) đã nói tới, phần lớn dữ liệu thực tế ở trạng thái không có phân phối chuẩn đa biến. Chính vì vậy, nhiều nhà nghiên cứu chấp nhận điều này và tiến hành phân tích SEM mà không cần xét tới dữ liệu có hay không có phân phối chuẩn đa biến.
(3) Không phải không có phân phối chuẩn thì SEM sẽ cho ra kết quả "vô dụng"
Việc dữ liệu không hoàn toàn tuân theo phân phối chuẩn không phải là rào cản quá lớn để thực hiện phân tích thống kê. Mặc dù phương pháp Maximum Likelihood sử dụng mặc định trong AMOS thường giả định phân phối chuẩn, nhưng đây không phải là một yêu cầu tuyệt đối. Việc vi phạm giả định này có thể ảnh hưởng đến kết quả phân tích, nhưng không nhất thiết làm cho kết quả trở nên vô dụng. Bởi vì phương pháp Maximum Likelihood trong ước lượng mô hình độ bền tương đối tốt đối với sự vi phạm giả định về phân phối chuẩn."Độ bền" ở đây mang ý nghĩa là ngay cả khi dữ liệu không hoàn toàn chuẩn, các ước lượng vẫn có thể cung cấp kết quả khá chính xác.
Một số chỉ số thống kê trong AMOS, như chỉ số phù hợp mô hình, thường không chênh lệch nhiều với sự vi phạm giả định về phân phối chuẩn đa biến.
Kiểm định ý nghĩa thống kê hệ số hồi quy trong SEM-Maximum Likelihood qua giá trị tới hạn C.R và trị số ý nghĩa P-value dựa trên phân phối chuẩn của dữ liệu. Chính vì vậy, đây là phần sẽ bị ảnh hưởng nhiều nếu mức độ vi phạm phân phối chuẩn là quá lớn. Chúng ta có thể hạn chế điều này bằng cách tăng lượng mẫu nghiên cứu lớn để phục vụ cho phân tích SEM. Bởi vì khi mẫu nghiên cứu lớn, dữ liệu sẽ có xu hướng tiến gần về phân phối chuẩn hơn.
Tóm lại, về nguyên tắc khi phân tích quan hệ trong mô hình bằng SEM trên AMOS, chúng ta cần theo thứ tự quy trình:
Bước 1: Đánh giá giả định phân phối chuẩn đa biến của dữ liệu
Bước 2: Chia làm 2 trường hợp:
- Nếu dữ liệu đảm bảo phân phối chuẩn đa biến, tiến hành phân tích SEM-Maximum Likelihood mặc định.
- Nếu dữ liệu không đảm bảo phân phối chuẩn đa biến, tiến hành phân tích SEM-Bootstrap.
4. Ứng dụng khác của kiểm định Bootstrap trên AMOS
Một ứng dụng phổ biến của kiểm định Bootstrap trên AMOS chính là phân tích biến trung gian (quan hệ gián tiếp) trong mô hình.
Kết quả từ kiểm định Bootstrap sẽ cung cấp 2 cách đánh giá ý nghĩa quan hệ trung gian:
1. Khoảng tin cậy Bootstrap của quan hệ trung gian: Kiểm tra khoảng tin cậy Bootstrap của tác động trung gian. Nếu khoảng tin cậy này không chứa giá trị 0, có thể kết luận rằng biến trung gian có vai trò ý nghĩa thống kê trong mô hình.
2. Giá trị sig Bootstrap của quan hệ trung gian: Dựa vào giá trị sig Bootstrap quan hệ trung gian và so sánh với mức ý nghĩa (ví dụ 0.05).
Xem chi tiết bài phân tích quan hệ trung gian bằng Bootstrap trên AMOS tại đây.