Hồi quy nhị phân là một phương pháp thống kê được sử dụng để mô hình hóa mối quan hệ giữa một biến phụ thuộc có tính nhị phân (có hai giá trị có thể là 0 hoặc 1) và một hoặc nhiều biến độc lập. Nó thường được sử dụng để dự đoán xác suất một sự kiện xảy ra hoặc không xảy ra dựa trên các biến độc lập.
1. Đặc điểm hồi quy nhị phân
Trong hồi quy nhị phân, biến phụ thuộc thường là biến nhị phân, ví dụ như "có" hoặc "không", "thành công" hoặc "thất bại", "1" hoặc "0". Điều này thường phản ánh các tình huống như "mua" hoặc "không mua", "đậu" hoặc "rớt", "đau" hoặc "không đau".
Mô hình hồi quy nhị phân sử dụng các phương trình hồi quy để tạo ra một dự đoán về xác suất của biến phụ thuộc bằng cách kết hợp các giá trị của các biến độc lập. Hàm sigmoid thường được sử dụng để chuyển đổi đầu ra của mô hình thành một giá trị xác suất nằm trong khoảng từ 0 đến 1.
Khi biến phụ thuộc ở dạng nhị phân thì không thể phân tích với dạng hồi quy thông thường vì nó sẽ vi phạm các giả định, dễ thấy nhất là khi biến phụ thuộc chỉ có hai biểu hiện thì không phù hợp khi giả định rằng phần dư có phân phối chuẩn, mà thay vào đó nó sẽ có phân phối nhị thức, điều này sẽ làm mất hiệu lực thống kê của các kiểm định trong phép hồi quy thông thường.
2. Phương trình hồi quy nhị phân
Thay vì chúng ta ước lượng giá trị của biến phụ thuộc Y theo biến độc lập X như ở hồi quy đa biến, thì trong hồi quy Binary Logistic, chúng ta sẽ ước lượng xác suất xảy ra sự kiện Y (probability) khi biết giá trị X. Biến phụ thuộc Y có hai giá trị 0 và 1, với 0 là không xảy ra sự kiện và 1 là xảy ra sự kiện. Phương trình hồi quy nhị phân Binary Logistic có dạng:
Trong đó:
Ứng dụng rất mạnh của hồi quy nhị phân Binary Logistic là khả năng dự báo. Từ phương trình hồi quy, chúng ta có phương trình mô hình hàm dự báo như sau:
Trong đó Pi = E(Y = 1/X) = P(Y = 1) gọi là xác suất để sự kiện xảy ra (Y = 1) khi biến độc lập X có giá trị cụ thể Xi .
3. Đánh giá độ phù hợp mô hình hồi quy Binary Logistics trên SPSS
3.1 Kiểm định giả thuyết độ phù hợp mô hình
Trong hồi quy tuyến tính, chúng ta sử dụng kiểm định F để kiểm định giả thuyết độ phù hợp mô hình, còn với hồi quy Binary Logistic chúng ta sẽ sử dụng kiểm định Chi-square.
Hướng tiếp cận của kiểm định Chi-square đó là so sánh sự khác biệt giá trị -2LL giữa mô hình hồi quy trống và mô hình hồi quy được đề xuất, nếu mô hình đề xuất có -2LL thấp hơn mô hình trống sẽ là kết quả tốt. Trong SPSS, kết quả tính toán của mô hình hồi quy trống sẽ được thể hiện ở Block 0. Sau đó, các biến độc lập được đưa vào mô hình tạo nên mô hình hồi quy đề xuất. SPSS sẽ xử lý mô hình hồi quy đề xuất và đánh giá xem có sự khác biệt có ý nghĩa thống kê trị số -2LL giữa mô hình trống với mô hình đề xuất hay không, kết quả đánh giá sẽ được thể hiện ở Block 1.
Các số liệu của kiểm định Chi-square được lấy từ bảng Omnibus Tests of Model Coefficients. Bảng này sẽ có ba mục: Step, Block, Model. Chúng ta sẽ chú trọng vào kết quả kiểm định Chi-square ở mục Model, hai mục Step và Block chúng ta sẽ đánh giá bổ sung thêm cho Model nếu sử dụng các phép đưa biến vào là Forward, Backward.
Nếu giá trị sig kiểm định Chi-square ở hàng Model nhỏ hơn 0.05 (nếu đề tài sử dụng mức ý nghĩa 5%), mô hình hồi quy là phù hợp. Nếu giá trị sig này lớn hơn 0.05, mô hình hồi quy không phù hợp, bạn sẽ cần đánh giá lại biến đầu vào, dữ liệu đầu vào của nghiên cứu.
3.3 Hệ số -2 Log-Likelihood (-2LL)
Giá trị -2 log-likelihood được viết tắt là -2LL. Trị số -2LL có giá trị nhỏ nhất là 0 và không có giá trị lớn nhất. -2LL thường ứng dụng để so sánh giữa mô hình hồi quy trống (Null Model) và mô hình hồi quy được đề xuất (Proposed Model), nếu mô hình đề xuất có -2LL thấp hơn mô hình trống thì kết quả hồi quy là tốt (Hair và cộng sự, 2014).
Mô hình hồi quy trống nghĩa là không có biến độc lập nào được đưa vào mô hình. Mô hình hồi quy đề xuất là mô hình có sự xuất hiện của các biến độc lập. Tùy vào phép đưa biến (Enter hay Stepwise) mà sẽ có một hay nhiều mô hình hồi quy đề xuất, nhưng thường chúng ta xét đến mô hình hồi quy đề xuất cuối cùng.
Giá trị -2LL của mô hình hồi quy trống được ký hiệu trong SPSS là Initial -2 Log Likelihood. Ví dụ ở bàng trên -2LL = 412.027.
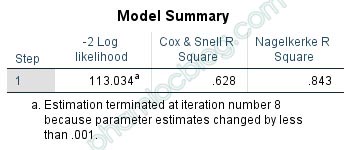
Giá trị -2LL của mô hình hồi quy đề xuất nằm ở bảng Model Summary tại cột -2 Log Likelihood. Ví dụ ở bàng trên -2LL = 144.696. Dễ dàng thấy được 144.696 < 412.027, như vậy, mô hình hồi quy phù hợp.
Về bản chất, việc so sánh -2LL giữa mô hình hồi quy trống với mô hình đề xuất không thực sự cần thiết. Bởi kiểm định Chi-square độ phù hợp mô hình ở mục 3.1 đã làm điều này rồi, và tính chính xác của việc đánh giá bằng kiểm định Chi-square sẽ cao hơn so với việc so sánh độ lớn -2LL. Khi sig kiểm định Chi-square ở hàng Model nhỏ hơn 0.05, điều này đồng nghĩa -2LL của mô hình đề xuất đã nhỏ hơn đáng kể so với mô hình trống.
3.3 Hệ số Cox & Snell R Square và Nagelkerke R Square
Kiểm định độ phù hợp mô hình bằng Chi-square cho chúng ta biết được mô hình có phù hợp hay không nhưng không nói lên được mức độ phù hợp nhiều hay ít. Chình vì vậy, các nhà nghiên cứu đã xây dựng giá trị “R Square giả” (Pseudo R Square) dựa theo tính chất R Square trên hồi quy tuyến tính (Hair và cộng sự, 2014) để đánh giá mức độ phù hợp của hồi quy nhị phân.
Hai giá trị R Square cho hồi quy Binary Logistic mà SPSS sử dụng dựa trên nghiên cứu của Cox & Snell (1989) và Nagelkerke (1991) . Theo công thức tính, hệ số Cox & Snell R Square sẽ không thể đạt tới giá trị lớn nhất là 1. Vì vậy, Nagelkerke đã đưa ra thêm một chỉ số R Square khác có giá trị dao động từ 0 đến 1. Cả hai trị số R Square này nếu càng lớn thì mô hình hồi quy càng tốt. Lưu ý rằng:
- Không có ngưỡng R bình phương bao nhiêu là cao, bao nhiêu là thấp. Hai giá trị R bình phương này càng tiến về 1 thì mô hình có độ phù hợp càng cao.
- Giá trị R bình phương ở đây không giống như R bình phương trên hồi quy tuyến tính. Giá trị R bình phương trong hồi quy nhị phân không biểu thị mức độ giải thích của các biến độc lập lên biến phụ thuộc.
3.4 Kiểm định giả thuyết ý nghĩa hệ số hồi quy
Trong hồi quy tuyến tính, chúng ta sử dụng kiểm định t để kiểm định giả thuyết ý nghĩa của hệ số hồi quy, còn với hồi quy Binary Logistic chúng ta sẽ sử dụng kiểm định Wald.
Nếu giá trị sig kiểm định Wald nhỏ hơn 0.05 (nếu đề tài sử dụng mức ý nghĩa 5%), biến độc lập có ý nghĩa trong mô hình hồi quy. Nếu giá trị sig này lớn hơn 0.05, biến độc lập đó không có ý nghĩa.
Nếu hệ số hồi quy B mang dấu âm, biến độc lập có tác động nghịch, nếu mang dấu dương, biến độc lập có tác động thuận.
Trong SPSS, các số liệu của kiểm định Wald được lấy từ bảng Variables in the Equation. Cũng lưu ý rằng, nếu một biến độc lập không có ý nghĩa thống kê trong kết quả hồi quy, chúng ta sẽ kết luận biến độc lập đó không có sự tác động lên biến phụ thuộc mà không cần thực hiện loại biến và phân tích lại hồi quy.
4. Phân tích hồi quy nhị phân Binary Logistics trên SPSS
Thực hiện phân tích hồi quy nhị phân bằng SPSS ở ví dụ dưới dây. Đây là nghiên cứu của một ngân hàng nhằm xem xét khả năng trả nợ của các cá nhân để quyết định có nên cho họ vay vốn hay không. Biến phụ thuộc TraNo mang 2 giá trị: 0 biểu hiện ý nghĩa không trả được nợ và 1 biểu hiện ý nghĩa trả được nợ. Có 3 biến độc lập trong mô hình tác động lên biến phụ thuộc TraNo gồm:
- Trình độ học vấn (HocVan): số năm đi học.
- Độ tuổi (Tuoi): số tuổi đến hiện tại.
- Thu nhập hàng tháng (ThuNhap): mức thu nhập hàng tháng tính bằng triệu đồng.
Lưu ý, với biến độc lập là biến định tính phân thành nhóm, chúng ta cần mã hóa chúng về biến giả Dummy rồi mới thực hiện hồi quy. Cách mã hóa mời các bạn xem tại bài viết: Hồi quy với biến độc lập định tính (biến giả Dummy) trên SPSS.
Nếu các biến độc lập ở dạng thang đo gồm nhiều biến quan sát con cấu thành nên, chúng ta cần tình trung bình cộng hoặc tính tổng các biến quan sát để tạo ra biến đại diện mới đưa vào phân tích.
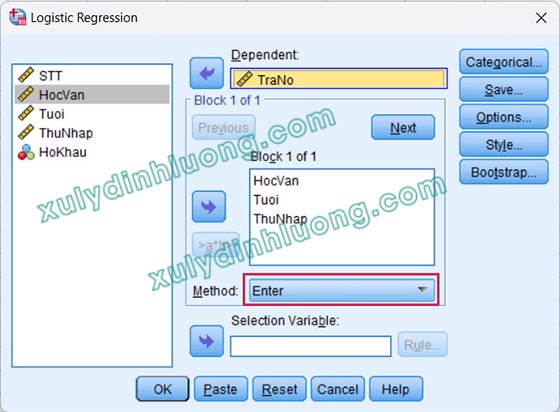
Thực hiện hồi quy nhị phân trên phần mềm SPSS. Chúng ta vào Analyze > Regression > Binary Logistic…
Đưa biến phụ thuộc Y vào mục Dependent, đưa các biến độc lập vào mục Covariates.
Tại tùy chọn Options, tích vào mục Iteration history, chọn Continue để quay lại cửa sổ ban đầu.
Tại mục Method, chọn phương pháp Enter. Tiếp tục nhấp vào OK để xuất các bảng kết quả.
5. Đọc kết quả hồi quy nhị phân Binary Logistics trên SPSS
Bảng Case Processing Summary cho chúng ta các thông tin mô tả đặc điểm dữ liệu đưa vào phân tích hồi quy nhị phân. Cụ thể ở đây, có 300 quan sát (cỡ mẫu hợp lệ) được đưa vào phân tích (Included in Analysis), không có quan sát nào bị thiếu số liệu (Missing Cases), không có quan sát nào không được chọn (Unselected Cases).
Bảng Dependent Variable Encoding cho biết biến phụ thuộc đang mang 2 giá trị, "Không trả được nợ" mã hóa là 0 và "Trả được nợ" mã hóa là 1.
Phần tiếp theo là kết quả ở Block 0. Chúng ta sẽ bỏ qua phần này bởi vì các kết quả phân tích ở Block 0 nằm ở trường hợp không có bất kỳ biến độc lập nào được đưa vào mô hình. Chúng ta sẽ đọc kết quả phân tích ở Block 1.Bảng đầu tiên là Omnibus Tests of Model Coefficients. Bảng này cho kết quả phân tích các hệ số của mô hình. Step 1 là bước thứ nhất trong chạy mô hình Logistic. Do ở đây chúng ta dùng phương pháp Enter đưa các biến độc lập vào cùng một lần nên chỉ xuất hiện Step 1 trong kết quả thống kê. Trường hợp dùng các phương pháp khác bảng này sẽ có thêm các Step 2, 3, 4 tùy số lượng biến đưa vào.
Cột Chi-square và Sig. thể hiện kết quả của kiểm định Chi bình phương, đây là kiểm định để đánh giá giả thuyết sự phù hợp của mô hình hồi quy. Giá trị sig kiểm định Chi-square ở hàng Model bằng 0.000 < 0.05, do đó, mô hình hồi quy là phù hợp.
Bảng tiếp theo là Model Summary cho kết quả mức độ phù hợp của mô hình.
Bảng thứ ba là Classification Table cho thấy phân loại đối tượng trả được nợ và không trả được nợ theo hai tiêu chí: quan sát thực tế và dự đoán. Ý nghĩa:
- Trong 129 trường hợp quan sát không trả được nợ, thì dự đoán có 122 trường hợp không trả được, tỉ lệ dự đoán đúng là 122/129 = 94.6%.
- Trong 171 trường hợp quan sát trả được nợ, dự đoán có 168 trường hợp trả được, tỉ lệ dự đoán đúng là 168/171 = 98.2%.
Như vậy, tỷ lệ trung bình dự đoán đúng là (122+168)/(122+168+3+7) = 96.7%.
Bảng cuối cùng là Variables in the Equation cho chúng ta kết quả kiểm định Wald, hệ số hồi quy và Exp(B) từng biến độc lập.
Giá trị sig kiểm định Wald của Tuoi, ThuNhap nhỏ hơn 0.05, như vậy hai biến này có sự ảnh hưởng lên khả năng trả nợ. Biến HocVan có sig kiểm định Wald bằng 0.278 > 0.05, HocVan không có sự tác động lên khả năng trả nợ.
Hệ số hồi quy B của Tuoi, ThuNhap đều mang dấu dương, điều này đồng nghĩa khi tuổi và thu nhập cao hơn thì khả năng trả nợ cao hơn.
Lưu ý rằng, trong hồi quy nhị phân không có hệ số hồi quy chuẩn hóa, do đó chúng ta không đánh giá thứ tự tác động của các biến độc lập.
Với kết quả ở trên, thế vào phương trình hồi quy ta có (trường hợp biến độc lập có Sig kiểm định Wald > 0.05 sẽ không được đưa vào phương trình hồi quy):
6. Ứng dụng dự báo của hồi quy nhị phân Binary Logistic
Một điểm rất mạnh của hồi quy nhị phân đó chính là khả năng dự báo. Sử dụng ví dụ ở trên, giả sử có anh Nguyễn Văn A đến ngân hàng vay vốn, hanh A cung cấp đầy đủ các thông tin như sau:
- Độ tuổi: 35 tuổi
- Thu nhập: 17 triệu/tháng
Thế vào phương trình mô hình dự báo ta có:
Mô hình Binary Logistic cho biết khả năng trả được nợ của người này là 94.26% > 50%. Như vậy ngân hàng nên cho anh A vay vì khả năng trả nợ của anh A là rất tốt.
--------
Nếu bạn gặp khó khăn khi thực hiện phân tích hồi quy nhị phân do biến bị loại nhiều, mô hình không đạt độ phù hợp, bạn có thể tham khảo dịch vụ chạy thuê SPSS của Phạm Lộc Blog hoặc liên hệ trực tiếp email xulydinhluong@gmail.com.